The Math Behind Momentum
Next, let's look at the math that allows us to calculate the stopping distance for a train. Like all vehicles, trains are stopped by braking, and braking relies on friction between the wheels and the track. Therefore, the greater the frictional traction with the track, the more rapidly the train will be able to stop. You can immediately see the great danger posed by ice, snow, dirt, etc. Just as with an automobile on the road, a train with reduced traction against the track will be unable to stop.
Remember from previous lessons that the maximum amount of friction between surfaces (like train wheels on steel rails) depends on the normal force, which is equal (but opposite in direction) to the weight of the train. Remember also that maximum frictional force is characterized by a coefficient of friction (denoted 
- pronounced "mew"). Values between 
and 
would be typical for trains under reasonably good track conditions. As soon as the train engineer hits the brakes, we will assume that the train quickly achieves maximum possible braking friction. Just as with the ABS systems ("automatic braking systems") of new cars, modern trains are assisted by computer to help them brake using as much friction as possible. If the wheels lose traction and begin to skid, computerized controls automatically ease off the braking until frictional traction is regained.
The smallest achievable braking distance is given by the following math equation:
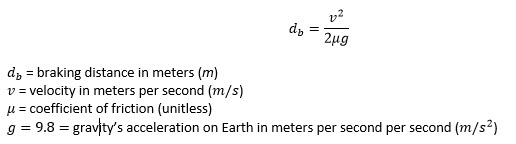
If you are wondering why Earth's gravity plays a role, it's NOT because gravity is helping to slow down the train - only the brakes do that on horizontal ground. Rather, it's because gravity is responsible for the weight of the train, which is connected to the friction that slows the train down.