Not only does it take a lot of force and quite a bit of time (and therefore distance) to accelerate big vehicles like trains, but it also takes a lot of force and time and distance to stop them. Imagine the force required to slow down and stop a train weighing 20,000 tons that's traveling at 80mph, when the engineer sees that there is an automobile stuck on the tracks ahead! Exactly how much force would that take? How much stopping time would be required, and how much stopping distance? That's what this lesson is about.
As you might imagine, there are many factors involved in calculating the stopping distance required for such a massive vehicle. This lesson teaches the basic ideas.
Figure 3.3.1. It takes a lot of force, time, and distance to get trains up to speed--and also to stop them.
Imagine that you are at the controls of a Union Pacific locomotive. You are the engineer. As you come around a bend in the tracks, you suddenly see a car stuck on the railroad crossing ahead. The car is about a half-mile away. Can you stop in time, or are you going to crash into it?
In 2013 alone, this very situation resulted in 2087 collisions between trains and automobiles. So hopefully the importance of stopping time and stopping distance is self-evident. (And also, be careful driving your car, especially when it comes to railroad crossings!)
We need to begin this lesson with an important physics concept called momentum. Momentum is the product of an object's mass and its velocity. The SI unit for momentum is the 
. In a math equation, the formula for momentum is:
p = mv
= momentum in kilogram∙meters per second (
)*
= mass in kilograms ( 
)
= velocity in meters per second (
)
_____________________________________________________________________________________________________
Note: p might seem like a strange abbreviation for momentum. Perhaps it is, but m isn't available since it already stands for mass. The concept of momentum was discovered by Sir Isaac Newton (1643-1727), English Physicist and father of modern physics. But he referred to it by the awkward phrase "quantity of motion." A contemporary of Newton's, the German mathematician Gottfried Leibniz (1646-1716), coined the more elegant term "progress" - and there lies the origin of the abbreviation p. Today we call the concept "momentum," but the p from "progress" persists as its abbreviation.
_____________________________________________________________________________________________________
Here is a table and a graph of an objects momentum based on its mass, assuming the object is a freight train moving at a constant (unchanging) speed of 
(
):
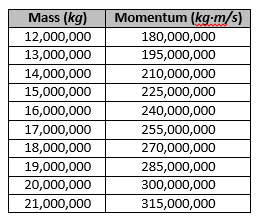
Figure 3.3.2. As you can see from this table, as mass increases, momentum increases.
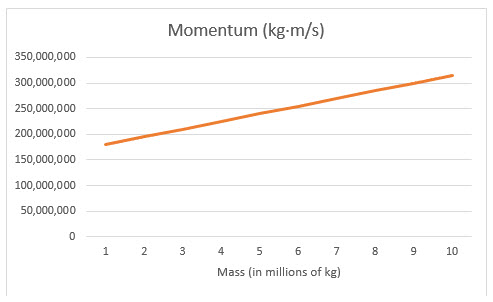
Figure 3.3.3. This chart shows the relationship between mass and momentum visually.
Below is a table and graph of an object's momentum based on its velocity, assuming the object is a golf ball with a mass of 
(
):
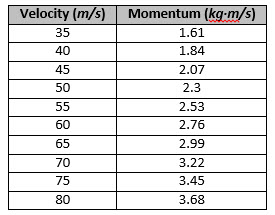
Figure 3.3.4. Here you see the relationship between velocity and momentum. Notice that as velocity rises, so does momentum.
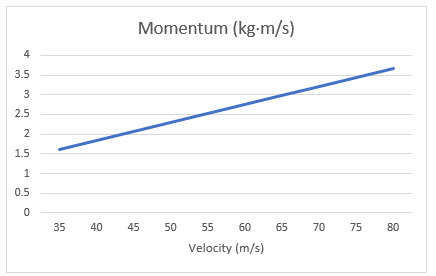
Figure 3.3.5. This graph shows the positive correlation between velocity and momentum.
What do these graphs tell us? Two things... As mass increases, momentum increases. And, as velocity increases, momentum also increases. So momentum serves as a measurement of the overall "quantity of motion" in an object - it increases both as the object moves faster, and also when the object has more mass.
Click the link that appears below to get some more information about momentum:
The more momentum an object has, the harder it is to stop. Therefore, something big and fast like a freight train is going to take a LONG TIME to stop!
Next, let's look at the math that allows us to calculate the stopping distance for a train. Like all vehicles, trains are stopped by braking, and braking relies on friction between the wheels and the track. Therefore, the greater the frictional traction with the track, the more rapidly the train will be able to stop. You can immediately see the great danger posed by ice, snow, dirt, etc. Just as with an automobile on the road, a train with reduced traction against the track will be unable to stop.
Remember from previous lessons that the maximum amount of friction between surfaces (like train wheels on steel rails) depends on the normal force, which is equal (but opposite in direction) to the weight of the train. Remember also that maximum frictional force is characterized by a coefficient of friction (denoted 
- pronounced "mew"). Values between 
and 
would be typical for trains under reasonably good track conditions. As soon as the train engineer hits the brakes, we will assume that the train quickly achieves maximum possible braking friction. Just as with the ABS systems ("automatic braking systems") of new cars, modern trains are assisted by computer to help them brake using as much friction as possible. If the wheels lose traction and begin to skid, computerized controls automatically ease off the braking until frictional traction is regained.
The smallest achievable braking distance is given by the following math equation:
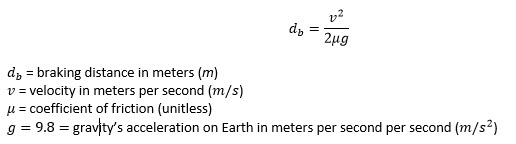
If you are wondering why Earth's gravity plays a role, it's NOT because gravity is helping to slow down the train - only the brakes do that on horizontal ground. Rather, it's because gravity is responsible for the weight of the train, which is connected to the friction that slows the train down.
On the last page, we saw that the smallest achievable braking distance is given by the following math equation:
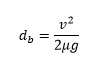
But... this only accounts for what happens after the brakes are applied. We also have to consider a factor called perception-reaction time, which is time required for the train engineer to recognize the need to stop, and to trigger the brakes. On average, perception-reaction time has been determined to be approximately 1 second. This means that if you were the train engineer, you would see the car stuck on the tracks ahead and react to it in approximately 1 second. How far would your train travel in that amount of time, during which you were moving toward the brakes? Here is the equation for the distance traveled during perception-reaction time:
When we put these last two equations together, we get a basic equation for the total stopping distance required to stop the train once you've seen the car stuck on the tracks:
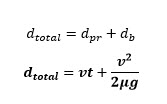
Let's take a look at how to apply the stopping distance equation introduced on the previous page.
You are the engineer of a freight train rolling along at 
, when you get a call on the radio that there's a herd of cows ahead on the track, about a quarter-mile (1/4 mile) away. Your perception-reaction time is 1 second, and the track conditions allow for a friction coefficient of 
. Will you be able to get your train stopped in time?
Step 1 - convert mph (miles per hour, the English velocity unit) to m/s (meters per second, the SI velocity unit). Note: you wouldn't always have to do this, since you might be given meters per second in the first place - but for now it's good practice.
Step 3 - convert meters back to miles for interpretation.
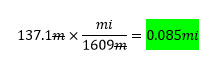
We find that 1/4 mile IS a sufficient stopping distance (the cows are safe) as long as your perception-reaction time is within 1 second, and you brake the train with maximum possible friction under good track conditions. Otherwise, the cows could be in greater danger.
For the last section of this lesson, let's relate the momentum of a moving object to the braking time and friction.
Here's the math equation by which we can calculate the braking (frictional) force:
See if you can figure out how to express this equation as a sentence, and what it means. You'll be asked this question on your assignment for the lesson.
However, notice that we have problem - there are two values that we don't know in the equation above. We don't know the stopping force (F), and we also don't know the braking time (t). So we'll need a 2nd math equation that allows us to find braking time from braking distance. Here it is:
Let's practice using the equations introduced on the last page.
You have been informed about some cows in the middle of the tracks ahead, and you have hit the brakes on your 
train moving at 
( 
) with a friction coefficient of 
. How long will it take the train take to stop? How much force will the brakes exert on the train in the process?
In Example 1 we calculated that a minimum stopping distance of 
will be required. However, be careful! This stopping distance included the distance traveled during perception-reaction time. To find braking time we need to know the braking distance, which does NOT include perception-reaction time. So we'll need to calculate the braking distance first.
Step 1 - Calculate braking distance.
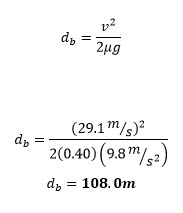
Step 2 - Now we can calculate braking time from braking distance.
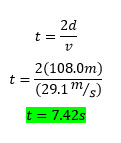
Step 3 - Finally we can use stopping time to determine braking (frictional) force. Remember that momentum is calculated from 
, so we'll use that fact in the equation for braking force.
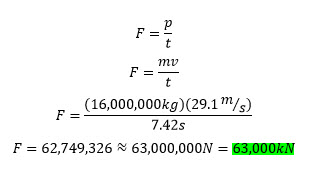
So we have determined that the train will stop in 7.42 seconds by braking with 63,000kN of force. That's quite a lot of force! But remember that the train has brakes all along its length, and the frictional force can therefore be spread out across many contact points between the wheels and the track.