Example of Calculating Braking Time
Let's practice using the equations introduced on the last page.
Example 2
You have been informed about some cows in the middle of the tracks ahead, and you have hit the brakes on your 
train moving at 
( 
) with a friction coefficient of 
. How long will it take the train take to stop? How much force will the brakes exert on the train in the process?
In Example 1 we calculated that a minimum stopping distance of 
will be required. However, be careful! This stopping distance included the distance traveled during perception-reaction time. To find braking time we need to know the braking distance, which does NOT include perception-reaction time. So we'll need to calculate the braking distance first.
Step 1 - Calculate braking distance.
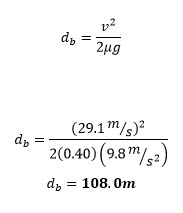
Step 2 - Now we can calculate braking time from braking distance.
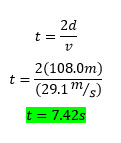
Step 3 - Finally we can use stopping time to determine braking (frictional) force. Remember that momentum is calculated from 
, so we'll use that fact in the equation for braking force.
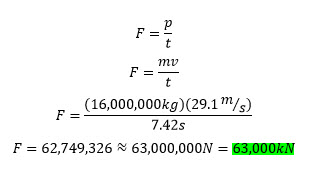
So we have determined that the train will stop in 7.42 seconds by braking with 63,000kN of force. That's quite a lot of force! But remember that the train has brakes all along its length, and the frictional force can therefore be spread out across many contact points between the wheels and the track.